Bom dia pessoal!
Nesta semana fizemos as últimas gravações referentes à video aula e ao podcast.
Está quase tudo pronto para a entrega na terça feira.
Abraços!
sexta-feira, 12 de novembro de 2010
sexta-feira, 29 de outubro de 2010
Vídeo sobre o Teorema de D'Alembert
Boa tarde pessoal!
No post de hoje iremos apresentar um vídeo explicativo sobre o Teorema de D'Alembert e passar a vocês informações atualizadas sobre o andamento do nosso trabalho sobre os polinômios.
A revista já começou a ser confeccionada e as vídeo aulas já estão sendo planejadas, em breve estaremos realizando as gravações e vamos colocar aqui no blog alguns trechos para que a turma já sinta um gostinho de como ficará o trabalho final.
O podcast será a última etapa.
Enquanto isso, acompanhem este interessante vídeo sobre o Teorema de D'Alembert.
Dessa vez, colocaremos direto o link do Youtube: http://www.youtube.com/watch?v=n_Ai-DdGaCQ
No post de hoje iremos apresentar um vídeo explicativo sobre o Teorema de D'Alembert e passar a vocês informações atualizadas sobre o andamento do nosso trabalho sobre os polinômios.
A revista já começou a ser confeccionada e as vídeo aulas já estão sendo planejadas, em breve estaremos realizando as gravações e vamos colocar aqui no blog alguns trechos para que a turma já sinta um gostinho de como ficará o trabalho final.
O podcast será a última etapa.
Enquanto isso, acompanhem este interessante vídeo sobre o Teorema de D'Alembert.
Dessa vez, colocaremos direto o link do Youtube: http://www.youtube.com/watch?v=n_Ai-DdGaCQ
quinta-feira, 21 de outubro de 2010
Teorema de D'Alembert
Retomando:
Exemplo:
O resto da divisão de m(x) = x³ - 5x² + x - 1 por h(x) = x - 7 = 0 --> x = 7
Resto r: m(7) = 7³ - 5 . 7² + 7 - 1 = 104, isto é, r = 104
Como consequência direta do teorema do resto, pode-se demonstrar outro teorema, conhecido como teorema de D'Alembert, em homenagem ao matemático francês Jean le Rond D'Alembert (1717 - 1783).
* Um polinômio p(x) é divisível por x - a se, e somente se, a é raiz de p(x), isto é, p(a) = 0.
Exemplo:
Vamos verificar se p(x) = x⁴ - 2x - 12 é divisível por h(x) = x - 2.
* raiz do divisor: x - 2 = 0 --> x = 2
* resto r: p(2) = 2⁴ - 2 . 2 - 12 = 0, isto é, r = 0
Portanto, p(x) é divisível por h (x).
Quem foi D'Alembert?
Jean le Rond d'Alembert foi um filósofo, matemático e físico francês, que participou na edição Encyclopédie, a primeira enciclopédia publicada na Europa.
Exemplo:
O resto da divisão de m(x) = x³ - 5x² + x - 1 por h(x) = x - 7 = 0 --> x = 7
Resto r: m(7) = 7³ - 5 . 7² + 7 - 1 = 104, isto é, r = 104
Como consequência direta do teorema do resto, pode-se demonstrar outro teorema, conhecido como teorema de D'Alembert, em homenagem ao matemático francês Jean le Rond D'Alembert (1717 - 1783).
* Um polinômio p(x) é divisível por x - a se, e somente se, a é raiz de p(x), isto é, p(a) = 0.
Exemplo:
Vamos verificar se p(x) = x⁴ - 2x - 12 é divisível por h(x) = x - 2.
* raiz do divisor: x - 2 = 0 --> x = 2
* resto r: p(2) = 2⁴ - 2 . 2 - 12 = 0, isto é, r = 0
Portanto, p(x) é divisível por h (x).
Quem foi D'Alembert?
Jean le Rond d'Alembert foi um filósofo, matemático e físico francês, que participou na edição Encyclopédie, a primeira enciclopédia publicada na Europa.
domingo, 10 de outubro de 2010
Exercícios Resolvidos
Em virtude do feriado, tivemos um transtorno e o post de quinta-feira acabou vindo só hoje. Para recuperar o tempo perdido, escolhemos um vídeo muito legal que retoma alguns dos conceitos básicos que já abordamos em nossas postagens e apresenta uma série de exercícios resolvidos pelo professor Edir Reis, do Colégio Cascavelense.
Prestem atenção no Teorema de D'Alembert, um dos nossos próximos assuntos aqui no blog. Essa semana estaremos acertando as datas e as informações referentes ao podcast, revista e vídeo aula.
Agora, acompanhem o vídeo!
Prestem atenção no Teorema de D'Alembert, um dos nossos próximos assuntos aqui no blog. Essa semana estaremos acertando as datas e as informações referentes ao podcast, revista e vídeo aula.
Agora, acompanhem o vídeo!
quinta-feira, 30 de setembro de 2010
Divisão por (x – a) - Parte II
No último post introduzimos o início do conteúdo, mostrando as aplicações do Teorema do Resto. Hoje, apresentaremos conceitos importantes e necessários para dar continuidade ao nosso conteúdo. Acompanhem.
De modo geral, para a divisão de polinômios por binômios do tipo x - a, com a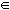
C, vale o seguinte teorema, chamado teorema do resto:
O resto r da divisão de um polinômio p(x) por um binômio do tipo x - a, com a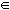 C, é igual a p(a), isto é, r = p(a).
Demonstrando:
De acordo com a definição de divisão, temos:
p(x) = (x - a) . q(x) + r(x), sendo q(x) o quociente e r(x) o resto.
Como x - a tem grau 1, o grau do resto é 0, isto é, o resto é nulo. Portanto, r(x) é um polinômio constante r. Então, podemos escrever a igualdade acima da seguinte forma:
p(x) = (x - a) . q(x) + r
Calculando p(a), temos:
p(a) = (a - a) . q(a) + r --> p(a) = r
Logo, o resto r da divisão é igual a p(a).
Exemplo:
O resto da divisão de m(x) = x³ - 5x² + x - 1 por h(x) = x - 7 é dado por:
Raiz do divisor: x - 7 = 0 --> x = 7
Resto r: m(7) = 7³ - 5 . 7² + 7 - 1 = 104, isto é, r = 104
Depois desta breve demonstração e do exemplo apresentado, acredito que os conceitos acerca do Teorema do Resto estejam mais claros a todos. No próximo post falaremos sobre o Teorema de D'Alembert, que, na realidade, trata-se de uma consequência direta do Teorema do Resto.
Na última segunda-feira começaram as aulas de reforço da 301, não deixe de frequentar!
Abraço!
De modo geral, para a divisão de polinômios por binômios do tipo x - a, com a
C, vale o seguinte teorema, chamado teorema do resto:O resto r da divisão de um polinômio p(x) por um binômio do tipo x - a, com a
C, é igual a p(a), isto é, r = p(a).Demonstrando:
De acordo com a definição de divisão, temos:
p(x) = (x - a) . q(x) + r(x), sendo q(x) o quociente e r(x) o resto.
Como x - a tem grau 1, o grau do resto é 0, isto é, o resto é nulo. Portanto, r(x) é um polinômio constante r. Então, podemos escrever a igualdade acima da seguinte forma:
p(x) = (x - a) . q(x) + r
Calculando p(a), temos:
p(a) = (a - a) . q(a) + r --> p(a) = r
Logo, o resto r da divisão é igual a p(a).
Exemplo:
O resto da divisão de m(x) = x³ - 5x² + x - 1 por h(x) = x - 7 é dado por:
Raiz do divisor: x - 7 = 0 --> x = 7
Resto r: m(7) = 7³ - 5 . 7² + 7 - 1 = 104, isto é, r = 104
Depois desta breve demonstração e do exemplo apresentado, acredito que os conceitos acerca do Teorema do Resto estejam mais claros a todos. No próximo post falaremos sobre o Teorema de D'Alembert, que, na realidade, trata-se de uma consequência direta do Teorema do Resto.
Na última segunda-feira começaram as aulas de reforço da 301, não deixe de frequentar!
Abraço!
quinta-feira, 23 de setembro de 2010
Divisão por (x – a) - Parte I
Iremos abordar a divisão por (x-a) aos poucos, para melhor entendimento de toda a turma. Nosso primeiro post sobre o assunto não virá do livro, e sim de um outro site bem bacana que resume uma importante atividade que necessita ser entendida, que é o Cálculo do Resto. Acompanhem:
Cálculo do Resto:
Na divisão de um polinômio P(x) por (x – a) observamos que o resto, se não for nulo, terá grau zero, isto é, será sempre um número real r. Então:
Feito isso, substituimos este 2 naquela equação que está sendo dividida, e temos como resultado, no primeiro exemplo, r = 7. Este "r" é o resto.
Como veremos, o grau do resto tem de ser menor que o grau do divisor. Lembrando que o grau de um polinômio não-nulo é o maior expoente da variável dentre os termos de coeficientes não-nulos. O grau do divisor é 1, pois o expoente de x é 1. Já o grau do resto é 0, pois não temos "x" no resto obtido.
Por hoje é isso aí pessoal. Espero que este breve comentário tenha esclarecido um pouco as dúvidas em relação ao Cálculo do Resto. Qualquer outro questionamento pode ser feito à um dos integrantes do grupo, Eduardo ou Bárbara. Outra forma de esclarecer eventuais dúvidas é comparecendo nas segundas-feiras à tarde no colégio, das 14h ás 15h. Estaremos lá.
Abraço!
Cálculo do Resto:
Na divisão de um polinômio P(x) por (x – a) observamos que o resto, se não for nulo, terá grau zero, isto é, será sempre um número real r. Então:
P(x) 
(x - a) · Q (x) + r
em que Q(x) é o quociente dessa divisão. Calculando o valor numérico de P(x) para x = a, temos:
P(a) = (a – a) · Q(a) + r
Logo, P(a) = r
Verificamos, assim, que:
1o) Calcular o resto da divisão de
P(x) = x4 – 3x2 + 2x – 1 por x – 2.
Resolução:
r = P(2) = 16 – 3 · 4 + 2 · 2 – 1
Assim, r = 7
2o) Calcular o resto da divisão de
P(x) = x4 + 2x3 + 3x2 – 6 por x + 2
Resolução:
x + 2 = x – (–2)
Então: r = P(–2)
r = (–2)4 + 2 (–2)3 + 3(–2)2 – 6
r = 6
Entenderam? Essa parte é bem fácil. É só você pegar o divisor, que, levando em conta o primeiro exemplo é x - 2 e isolar o x. Ficaria x = 2. Esse resultado é chamado de raiz do divisor.Feito isso, substituimos este 2 naquela equação que está sendo dividida, e temos como resultado, no primeiro exemplo, r = 7. Este "r" é o resto.
Como veremos, o grau do resto tem de ser menor que o grau do divisor. Lembrando que o grau de um polinômio não-nulo é o maior expoente da variável dentre os termos de coeficientes não-nulos. O grau do divisor é 1, pois o expoente de x é 1. Já o grau do resto é 0, pois não temos "x" no resto obtido.
Por hoje é isso aí pessoal. Espero que este breve comentário tenha esclarecido um pouco as dúvidas em relação ao Cálculo do Resto. Qualquer outro questionamento pode ser feito à um dos integrantes do grupo, Eduardo ou Bárbara. Outra forma de esclarecer eventuais dúvidas é comparecendo nas segundas-feiras à tarde no colégio, das 14h ás 15h. Estaremos lá.
Abraço!
sexta-feira, 17 de setembro de 2010
Apresentação
Boa tarde a todos. Me chamo Eduardo Wilsmann e venho por meio deste apresentar a vocês o nosso blog. Nosso porque ele não pertence apenas a mim e à Bárbara, como também a todos vocês.
Reuniremos aqui uma série de vídeo-aulas, resumos e explicações sobre a divisão de polinômios, focando principalmente na divisão por polinômios do tipo x-a.
Iremos estudar um caso particular de divisão de polinômios em que o dividendo é um polinômio com grau maior do que ou igual a 1 e o divisor é um polinômio de grau 1 do tipo x-a, com a pertencendo a C.
Espero que todos vocês gostem do blog e os convido para que desde já opinem na seção de comentários, enviando sugestões, dicas e/ou críticas construtivas.
Abraço!
Reuniremos aqui uma série de vídeo-aulas, resumos e explicações sobre a divisão de polinômios, focando principalmente na divisão por polinômios do tipo x-a.
Iremos estudar um caso particular de divisão de polinômios em que o dividendo é um polinômio com grau maior do que ou igual a 1 e o divisor é um polinômio de grau 1 do tipo x-a, com a pertencendo a C.
Espero que todos vocês gostem do blog e os convido para que desde já opinem na seção de comentários, enviando sugestões, dicas e/ou críticas construtivas.
Abraço!
Assinar:
Postagens (Atom)